How To Find Vertex From A Quadratic Equation

About Graphing Quadratic Functions

Quadratic function has the form $ f(x) = ax^2 + bx + c $ where a, b and c are numbers

Y'all tin can sketch quadratic function in four steps. I will explicate these steps in following examples.

Example 1:

Sketch the graph of the quadratic function

$$ {\color{blue}{ f(x) = x^2+2x-3 }} $$

Solution:

In this instance nosotros take $ a=one, b=2 $ and $c=-3$

Step 1: Find the vertex.

To detect ten - coordinate of the vertex we use formula:

$$ x=-\frac{b}{2a} $$

So, we substitute $one$ in for $a$ and $two$ in for $b$ to get

$$ ten=-\frac{b}{2a} = -\frac{2}{ii\cdot1} = -1 $$

To discover y - coordinate plug in $x=-1$ into the original equation:

$$ y = f(-1) = (-i)^two + 2\cdot(-1) - 3 = one - two - 3 = -iv $$

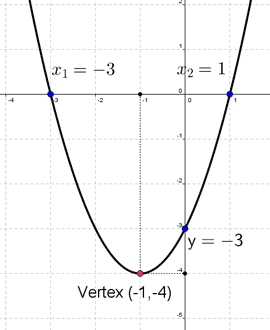
Then, the vertex of the parabola is $ {\color{red}{ (-ane,-4) }} $

Step 2: Find the y-intercept.

To find y - intercept plug in $x=0$ into the original equation:

$$ f(0) = (0)^two + 2\cdot(0) - 3 = 0 - 0 - 3 = -3 $$

And then, the y-intercept of the parabola is $ {\color{blue}{ y = -3 }} $

STEP iii: Observe the x-intercept.

To detect x - intercept solve quadratic equation $f(10)=0$ in our example we have:

$$ x^2+2x-3 = 0 $$

Solutions for this equation are:

$$ {\colour{blue}{ x_1 = -3 }} ~~~\text{and}~~~ {\color{blue}{ x_2 = 1 }} $$

( to learn how to solve quadratic equation utilize quadratic equation solver )

STEP 4: plot the parabola.

Example two:

Sketch the graph of the quadratic function

$$ {\color{blue}{ f(x) = -x^2+2x-ii }} $$

Solution:

Here we have $ a=-1, b=2 $ and $c=-2$

The x-coordinate of the vertex is:

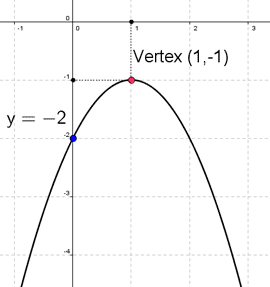
$$ {\color{bluish}{ x = -\frac{b}{2a} }} = -\frac{2}{2\cdot(-ane)}= ane $$

The y-coordinate of the vertex is:

$$ y = f(1) = -1^2+ii\cdot1-two = -1 + ii - ii = -1 $$

The y-intercept is:

$$ y = f(0) = -0^two+2\cdot0-ii = -0 + 0 - 2 = -2 $$

In this example x-intercept doesn't be since equation $-ten^2+2x-2=0$ does not has the solutions (use quadratic equation solver to check ). Then, in this case we will plot the graph using only two points

Source: https://www.mathportal.org/calculators/quadratic-equation/quadratic-function-grapher.php

Posted by: hillneho1973.blogspot.com

Share this post