How To Find The Gcf Of A Polynomial

four.2 Factoring Polynomials

Learning Objectives

1. Decide the greatest common factor (GCF) of monomials.
2. Factor out the GCF of a polynomial.
3. Factor a four-term polynomial by group.
4. Factor special binomials.

Determining the GCF of Monomials

The process of writing a number or expression as a production is called factoringThe procedure of writing a number or expression as a product. . If we write the monomial $8x^7=\mathrm{ii}{x}^5\cdot 4x^2$ , we say that the product $2x^5\cdot 4x^{\mathrm{ii}}$ is a factorizationWhatever combination of factors, multiplied together, resulting in the production. of $8x^7$ and that $\mathrm{ii}{\mathrm{ten}}^5$ and $4{\mathrm{ten}}^{\mathrm{ii}}$ are factorsAny of the numbers or expressions that course a production. . Typically, there are many ways to factor a monomial. Some factorizations of $8x^{\mathrm{vii}}$ follow:

$$\begin{array}{lll}\hfill \mathrm{eight}{x}^7& =\hfill & \mathrm{ii}{x}^5\cdot 4x^2\hfill \\ \hfill 8x^7& =\hfill & \mathrm{eight}{x}^6\cdot \mathrm{10}\hfill \\ \hfill 8x^{\mathrm{vii}}& =\hfill & 2x\cdot 2{\mathrm{ten}}^2\cdot \mathrm{ii}{x}^4\hfill \end{array}\}Factorizatio\mathrm{due\; north}sof\mathrm{viii}{x}^7$$

Given 2 or more monomials, it volition be useful to find the greatest common monomial factor (GCF)The product of the mutual variable factors and the GCF of the coefficients. of each. The GCF of the monomials is the product of the mutual variable factors and the GCF of the coefficients.

Example 1

Find the GCF of $25x^7{y}^{2}z$ and $15{\mathrm{ten}}^3{y}^{\mathrm{four}}{z}^2.$

Solution:

Begin by finding the GCF of the coefficients. In this case, $25=\mathrm{v}\cdot 5$ and $\mathrm{xv}=\mathrm{three}\cdot 5.$ It should be clear that

$$\text{GCF}\left(25,\mathrm{xv}\right)=5$$

Next determine the common variable factors with the smallest exponents.

$$25{\mathrm{10}}^7{y}^{2}z\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}and}15x^3{y}^4{z}^2$$

The common variable factors are ${\mathrm{10}}^3$ , $y^{\mathrm{two}}$ , and $z.$ Therefore, given the two monomials,

$$\text{GCF}=5{\mathrm{10}}^{\mathrm{iii}}{y}^{2}z$$

Answer: $5x^3{y}^{2}z$

Information technology is worth pointing out that the GCF divides both expressions evenly.

$$\frac{25{\mathrm{10}}^7{y}^{\mathrm{two}}z}{\mathrm{v}{x}^3{y}^{\mathrm{ii}}z}=\mathrm{five}{x}^4\text{and}\frac{15{\mathrm{ten}}^{\mathrm{three}}{y}^4{z}^2}{5x^{\mathrm{three}}{y}^{2}z}=3y^{2}z$$

Furthermore, nosotros can write the following:

$$25{\mathrm{ten}}^{\mathrm{seven}}{y}^{\mathrm{two}}z=5x^{\mathrm{three}}{y}^{2}z\cdot \mathrm{five}{x}^{\mathrm{iv}}\text{and}15x^3{y}^{\mathrm{iv}}{z}^2=\mathrm{v}{x}^3{y}^{\mathrm{two}}z\cdot 3y^{2}z$$

The factors $5{\mathrm{ten}}^{\mathrm{four}}$ and $3y^{2}z$ share no common monomial factors other than 1; they are relatively primeExpressions that share no common factors other than 1. .

Case 2

Determine the GCF of the following three expressions: $12a^5{b}^{\mathrm{ii}}{\left(a+b\right)}^5$ , $60a^{\mathrm{four}}{b}^{3}c{\left(a+b\right)}^3$ , and $24a^2{b}^{\mathrm{vii}}{c}^{\mathrm{three}}{\left(a+b\right)}^2.$

Solution:

Begin by finding the GCF of the coefficients. To practice this, determine the prime number factorization of each and then multiply the common factors with the smallest exponents.

$$\begin{array}{lll}\hfill 12& =\hfill & {\mathrm{ii}}^2\cdot \mathrm{three}\hfill \\ \hfill \mathrm{lx}& =\hfill & 2^2\cdot 3\cdot 5\hfill \\ \hfill 24& =\hfill & {\mathrm{two}}^3\cdot \mathrm{three}\hfill \end{array}$$

Therefore, the GCF of the coefficients of the three monomials is

$$\text{GCF}\left(12,60,24\right)={\mathrm{two}}^2\cdot 3=12$$

Side by side, determine the mutual factors of the variables.

$$12a^{\mathrm{five}}{b}^2{\left(a+b\right)}^{\mathrm{five}}\text{and}60a^4{b}^{3}c{\left(a+b\right)}^{\mathrm{iii}}\text{and}24a^{\mathrm{two}}{b}^7{c}^3{\left(a+b\right)}^2$$

The variable factors in common are $a^2$ , $b^2$ , and ${\left(a+b\right)}^2.$ Therefore,

$$\text{GCF}=12\cdot a^2\cdot b^{\mathrm{ii}}\cdot {\left(a+b\right)}^2$$

Notation that the variable c is not common to all 3 expressions and thus is not included in the GCF.

Answer: $12a^2{b}^2{\left(a+b\right)}^2$

Factoring out the GCF

The awarding of the distributive property is the key to multiplying polynomials. For example,

$$\begin{array}{lll}\hfill 6x{y}^2\left(2xy+\mathrm{i}\right)& =\hfill & 6x{y}^2\cdot 2xy+6\mathrm{10}{y}^2\cdot 1\mathrm{Thou}ultip\mathrm{fifty}yin\mathrm{thou}\hfill \\ \hfill & =\hfill & 12x^2{y}^{\mathrm{iii}}+\mathrm{half-dozen}x{y}^2\hfill \end{array}$$

The process of factoring a polynomial involves applying the distributive property in opposite to write each polynomial equally a product of polynomial factors.

$$\begin{array}{lll}\hfill a\left(b+c\right)& =\hfill & ab+ac\mathrm{1000}u\mathrm{50}tip\mathrm{50}ying\hfill \\ \hfill ab+ac& =\hfill & a\left(b+c\right)Factorin\mathrm{yard}\hfill \end{array}$$

Consider factoring the consequence of the opening example:

$$\begin{array}{lll}\hfill 12x^{\mathrm{ii}}{y}^3+6x{y}^2& =\hfill & \mathrm{six}x{y}^{\mathrm{two}}\cdot 2xy+6x{y}^2\cdot 1Factoring\hfill \\ \hfill & =\hfill & 6x{y}^2\left(?\right)\hfill \\ \hfill & =\hfill & 6x{y}^2\left(\mathrm{two}xy+\mathrm{ane}\right)\hfill \end{array}$$

We see that the distributive belongings allows u.s. to write the polynomial $12x^2{y}^3+\mathrm{six}x{y}^2$ as a product of the two factors $6\mathrm{10}{y}^{\mathrm{ii}}$ and $\left(2xy+1\right).$ Note that in this instance, $6x^{\mathrm{two}}y$ is the GCF of the terms of the polynomial.

$$\text{GCF}\left(12x^2{y}^3,6x{y}^2\right)=6x{y}^2$$

Factoring out the greatest common factor (GCF)The process of rewriting a polynomial as a production using the GCF of all of its terms. of a polynomial involves rewriting it as a product where a factor is the GCF of all of its terms.

$$\begin{array}{lll}\hfill \mathrm{eight}{x}^{\mathrm{three}}+\mathrm{iv}{x}^{\mathrm{two}}-16x& =\hfill & 4\mathrm{10}\left(\mathrm{ii}{x}^2+x-4\right)\hfill \\ \hfill 9a{b}^2-18a^{2}b-3ab& =\hfill & 3ab\left(3b-\mathrm{half-dozen}a-1\right)\hfill \end{array}\}Factori\mathrm{northward}\mathrm{thou}outtheGCF$$

To factor out the GCF of a polynomial, we kickoff determine the GCF of all of its terms. Then we tin can divide each term of the polynomial by this cistron as a means to determine the remaining cistron after applying the distributive holding in contrary.

Example 3

Cistron out the GCF: $18x^{\mathrm{seven}}-30x^{\mathrm{v}}+\mathrm{six}{\mathrm{10}}^3.$

Solution:

In this example, the GCF(eighteen, 30, 6) = 6, and the common variable cistron with the smallest exponent is $x^{\mathrm{three}}.$ The GCF of the polynomial is $6x^{\mathrm{iii}}.$

$$18{\mathrm{10}}^{\mathrm{vii}}-30x^{\mathrm{five}}+\mathrm{six}{x}^3=\mathrm{six}{x}^3\left(?\right)$$

The missing factor can exist establish by dividing each term of the original expression by the GCF.

$$\frac{18x^{\mathrm{vii}}}{6{\mathrm{10}}^3}=3x^{\mathrm{four}}\frac{-\mathrm{thirty}{x}^5}{6x^{\mathrm{three}}}=-5x^{\mathrm{ii}}\frac{+\mathrm{half-dozen}{x}^{\mathrm{iii}}}{\mathrm{half-dozen}{x}^3}=+1$$

Use the distributive holding (in reverse) using the terms found in the previous step.

$$\mathrm{xviii}{\mathrm{10}}^7-\mathrm{thirty}{\mathrm{10}}^5+\mathrm{half-dozen}{x}^3=\mathrm{six}{x}^3\left(3{\mathrm{ten}}^{\mathrm{four}}-5{\mathrm{ten}}^{\mathrm{two}}+1\right)$$

If the GCF is the aforementioned as one of the terms, so, subsequently the GCF is factored out, a constant term 1 will remain. The importance of remembering the constant term becomes clear when performing the check using the distributive property.

$$\begin{array}{lll}\hfill \mathrm{half\; dozen}{x}^3\left(3x^{\mathrm{iv}}-\mathrm{five}{\mathrm{10}}^2+1\right)& =\hfill & \mathrm{six}{\mathrm{10}}^3\cdot 3x^4-6x^{\mathrm{iii}}\cdot 5x^{\mathrm{two}}+6x^3\cdot \mathrm{one}\hfill \\ \hfill & =\hfill & 18{\mathrm{10}}^7-\mathrm{thirty}{x}^5+6x^3✓\hfill \end{array}$$

Respond: $6{\mathrm{ten}}^3\left(\mathrm{iii}{x}^{\mathrm{four}}-5x^{\mathrm{ii}}+\mathrm{i}\right)$

Example 4

Cistron out the GCF: $27{\mathrm{10}}^5{y}^{5}z+54x^{5}yz-63x^{\mathrm{iii}}{y}^{\mathrm{iv}}.$

Solution:

The GCF of the terms is $9{\mathrm{ten}}^{3}y.$ The terminal term does not take a variable factor of z, and thus z cannot exist a part of the greatest mutual factor. If we divide each term past $9x^{\mathrm{three}}y$ , we obtain

$$\frac{27{\mathrm{ten}}^5{y}^{5}z}{\mathrm{ix}{\mathrm{ten}}^{3}y}=\mathrm{iii}{x}^2{y}^{\mathrm{four}}z\frac{54x^{5}yz}{\mathrm{ix}{x}^{3}y}=6x^{2}z\frac{-63x^3{y}^4}{9x^{3}y}=-7y^3$$

and tin can write

$$\begin{array}{lll}\hfill 27{\mathrm{10}}^5{y}^{5}z+54x^{5}yz-63{\mathrm{10}}^3{y}^{\mathrm{four}}& =\hfill & 9x^{3}y\left(?\right)\hfill \\ \hfill & =\hfill & 9{\mathrm{ten}}^{3}y\left(\mathrm{iii}{x}^{\mathrm{ii}}{y}^{4}z+6{\mathrm{10}}^{2}z-7y^3\right)\hfill \end{array}$$

Reply: $9x^{3}y\left(3x^2{y}^{4}z+6x^{2}z-7y^3\right)$

Endeavor this! Factor out the GCF: $12x^3{y}^4-\mathrm{half-dozen}{\mathrm{ten}}^2{y}^3-3x{y}^{\mathrm{ii}}$

Respond: $3\mathrm{ten}{y}^2\left(\mathrm{iv}{x}^2{y}^{\mathrm{ii}}-2\mathrm{ten}y-1\right)$

Of grade, not every polynomial with integer coefficients can be factored as a product of polynomials with integer coefficients other than 1 and itself. If this is the case, and then we say that it is a prime polynomialA polynomial with integer coefficients that cannot be factored every bit a product of polynomials with integer coefficients other than one and itself. . For case, a linear factor such every bit $\mathrm{ten}x-9$ is prime. However, it can be factored every bit follows:

$$10x-9=x\left(10-\frac{\mathrm{ix}}{x}\right)\text{or}10x-9=5\left(\mathrm{ii}x-\frac{9}{5}\right)$$

If an x is factored out, the resulting factor is not a polynomial. If whatever abiding is factored out, the resulting polynomial factor will not accept integer coefficients. Furthermore, some linear factors are non prime. For example,

5x-10=5\left(\mathrm{10}-\mathrm{ii}\right)

In full general, whatsoever linear gene of the form $ax+b$ , where a and b are relatively prime integers, is prime number.

Factoring by Grouping

In this department, we outline a technique for factoring polynomials with four terms. Showtime, review a preliminary example where the terms have a common binomial factor.

Example 5

Gene: $7x\left(\mathrm{three}x-\mathrm{ii}\right)-\left(3x-2\right).$

Solution:

Begin by rewriting the 2nd term $-\left(\mathrm{three}\mathrm{ten}-\mathrm{two}\right)$ as $-1\left(3x-2\right).$ Next, consider $\left(3x-\mathrm{ii}\right)$ as a mutual binomial factor and factor it out as follows:

$$\begin{array}{lll}\hfill 7x\left(3x-2\right)-\left(\mathrm{iii}x-2\right)& =\hfill & 7x\left(\mathrm{iii}\mathrm{10}-2\right)-\mathrm{one}\left(3x-2\right)\hfill \\ \hfill & =\hfill & \left(3\mathrm{ten}-\mathrm{two}\right)\left(?\right)\hfill \\ \hfill & =\hfill & \left(3x-\mathrm{two}\right)\left(\mathrm{seven}x-\mathrm{one}\right)\hfill \end{array}$$

Answer: $\left(\mathrm{three}x-2\right)\left(7\mathrm{10}-1\right)$

Factoring by groupA technique for factoring polynomials with four terms. is a technique that enables us to factor polynomials with four terms into a product of binomials. This involves an intermediate step where a mutual binomial factor will be factored out. For example, we wish to factor

$$\mathrm{three}{x}^3-12x^{\mathrm{two}}+\mathrm{two}x-8$$

Brainstorm by grouping the first two terms and the last ii terms. Then factor out the GCF of each grouping:

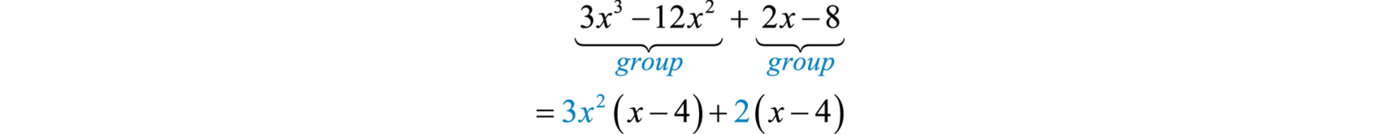
In this form, the polynomial is a binomial with a common binomial gene, $\left(x-\mathrm{four}\right).$

$$\begin{array}{l}\hfill =\left(x-\mathrm{iv}\right)\left(?\right)\\ \hfill =\left(\mathrm{10}-\mathrm{four}\right)\left(3x^2+\mathrm{ii}\right)\end{array}$$

Therefore,

$$3x^3-12x^{\mathrm{two}}+2x-8=\left(x-4\right)\left(3{\mathrm{10}}^{\mathrm{ii}}+2\right)$$

We can cheque by multiplying.

$$\begin{array}{lll}\hfill \left(x-4\right)\left(3x^{\mathrm{two}}+2\right)& =\hfill & \mathrm{iii}{x}^3+\mathrm{ii}x-12x^2-\mathrm{eight}\hfill \\ \hfill & =\hfill & 3x^{\mathrm{three}}-12{\mathrm{10}}^2+2x-8✓\hfill \end{array}$$

Example 6

Factor by grouping: $24a^{\mathrm{four}}-18a^3-20a+15.$

Solution:

The GCF for the commencement group is $6a^{\mathrm{three}}.$ Nosotros accept to choose five or −five to factor out of the second group.

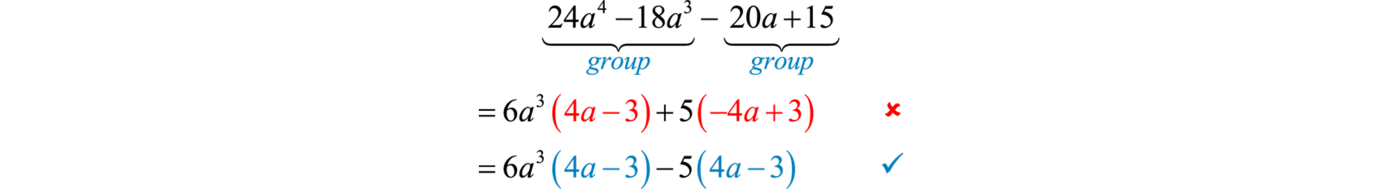
Factoring out +v does not event in a mutual binomial factor. If we cull to factor out −5, then we obtain a mutual binomial factor and can proceed. Note that when factoring out a negative number, nosotros change the signs of the factored terms.

Respond: $\left(4a-3\right)\left(\mathrm{vi}{a}^3-\mathrm{v}\right).$ Check by multiplying; this is left to the reader equally an practice.

Sometimes nosotros must showtime rearrange the terms in order to obtain a mutual factor.

Instance seven

Factor: $ab-2a^{2}b+a^3-\mathrm{two}{b}^2.$

Solution:

Merely factoring the GCF out of the first group and last group does not yield a common binomial cistron.

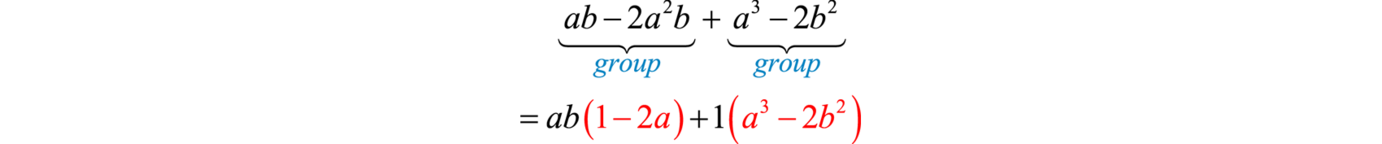
We must rearrange the terms, searching for a group that produces a common factor. In this example, we have a workable group if nosotros switch the terms $a^{\mathrm{three}}$ and $ab.$

Answer: $\left(a-2b\right)\left(a^2+b\right)$

Endeavour this! Factor: $x^{\mathrm{three}}-{\mathrm{10}}^{2}y-\mathrm{10}y+y^2.$

Answer: $\left(x-y\right)\left(x^2-y\right)$

Not all factorable four-term polynomials can exist factored with this technique. For example,

$$3x^3+\mathrm{v}{\mathrm{ten}}^{\mathrm{two}}-\mathrm{10}+2$$

This four-term polynomial cannot be grouped in any manner to produce a mutual binomial factor. Despite this, the polynomial is non prime and can exist written as a product of polynomials. Information technology tin be factored as follows:

$$3x^{\mathrm{iii}}+5{\mathrm{ten}}^2-\mathrm{ten}+\mathrm{two}=\left(\mathrm{10}+\mathrm{two}\right)\left(3x^2-x+\mathrm{one}\right)$$

Factoring such polynomials is something that we will learn to practise every bit we motion farther along in our study of algebra. For now, nosotros will limit our try to cistron iv-term polynomials to using the factor by grouping technique.

Factoring Special Binomials

A binomial is a polynomial with ii terms. We begin with the special binomial chosen divergence of squares $a^{\mathrm{two}}-b^2=\left(a+b\right)\left(a-b\right),$ where a and b correspond algebraic expressions. :

$$a^{\mathrm{ii}}-b^2=\left(a+b\right)\left(a-b\right)$$

To verify the above formula, multiply.

$$\begin{array}{lll}\hfill \left(a+b\right)\left(a-b\right)& =\hfill & a^2-ab+ba-b^2\hfill \\ \hfill & =\hfill & a^2-ab+ab-b^2\hfill \\ \hfill & =\hfill & a^2-b^2\hfill \end{array}$$

Nosotros use this formula to factor sure special binomials.

Example viii

Factor: $x^2-9y^2.$

Solution:

Place the binomial as difference of squares and determine the square factors of each term.

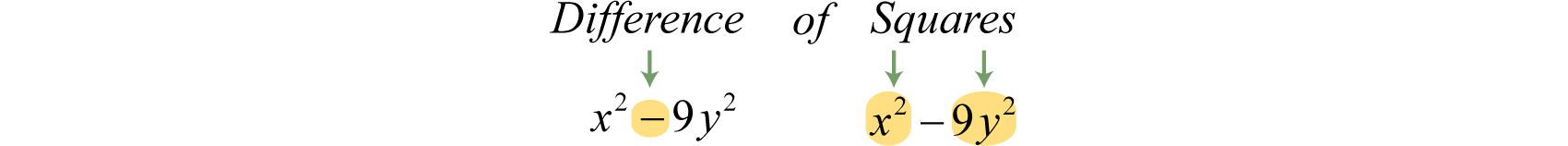
Hither we can write

$${\mathrm{ten}}^2-\mathrm{ix}{y}^2={\left(x\right)}^{\mathrm{two}}-{\left(\mathrm{iii}y\right)}^2$$

Substitute into the difference of squares formula where $a=\mathrm{ten}$ and $b=3y.$

$$\begin{array}{llllllllllll}\hfill a^2-b^{\mathrm{two}}& =\hfill & (\hfill & a& +& b& )& (& a& -& b& )\\ \hfill & \hfill & & \downarrow \hfill & & \downarrow & & & \downarrow & & \downarrow & \\ \hfill {\mathrm{10}}^2-9y^2& \hfill =\hfill & (\hfill & x& +& 3y& )& (& x& -& \mathrm{iii}y& )\end{array}$$

Multiply to check.

$$\begin{array}{ccc}\hfill \left(x+3y\right)\left(x-\mathrm{three}y\right)& =& x^2-\mathrm{iii}xy+3y\mathrm{ten}-9y^{\mathrm{ii}}\hfill \\ \hfill & =& {\mathrm{ten}}^2-3xy+\mathrm{iii}\mathrm{10}y-9y^2\hfill \\ \hfill & =& x^2-9y^2✓\hfill \end{array}$$

Respond: $\left(x+3y\right)\left(x-3y\right)$

Example nine

Factor: $x^{\mathrm{two}}-{\left(2\mathrm{10}-\mathrm{i}\right)}^{\mathrm{two}}.$

Solution:

Start, identify this expression every bit a difference of squares.

$$x^2-{\left(\mathrm{two}x-\mathrm{ane}\right)}^{\mathrm{two}}={\left(x\right)}^{\mathrm{two}}-{\left(\mathrm{ii}x-1\right)}^2$$

Utilize $a=x$ and $b=\mathrm{two}x-1$ in the formula for a difference of squares and then simplify.

$$a^2-b^2=\left(a+b\right)\left(a-b\right)$$

$$\begin{array}{ccc}\hfill x^2-{\left(2\mathrm{ten}-1\right)}^2& =& \left[\mathrm{10}+\left(2x-\mathrm{one}\right)\right]\left[x-\left(\mathrm{two}x-1\right)\right]\hfill \\ \hfill & =& \left(\mathrm{ten}+\mathrm{two}x-\mathrm{one}\right)\left(x-2x+1\right)\hfill \\ \hfill & =& \left(3x-1\right)\left(-\mathrm{ten}+1\right)\hfill \end{array}$$

Answer: $\left(3x-1\right)\left(-x+1\right)$

Given whatever existent number b, a polynomial of the form $x^2+b^2$ is prime. Furthermore, the sum of squares $a^2+b^2,$ where a and b correspond algebraic expressions. This does non have a general factored equivalent. $a^2+b^{\mathrm{two}}$ does non have a general factored equivalent. Care should be taken not to confuse this with a perfect square trinomial.

$$\begin{array}{lll}\hfill {\left(a+b\right)}^2& =\hfill & \left(a+b\right)\left(a+b\right)\hfill \\ \hfill & =\hfill & a^2+ab+ba+b^{\mathrm{two}}\hfill \\ \hfill & =\hfill & a^{\mathrm{two}}+2ab+b^{\mathrm{two}}\hfill \end{array}$$

Therefore,

$${\left(a+b\right)}^2\ne a^{\mathrm{ii}}+b^2$$

For example, the sum of squares binomial $x^2+\mathrm{ix}$ is prime. 2 other special binomials of interest are the sum $\begin{array}{l}{a}^3+b^3\hfill \\ =(a+b)(a^{\mathrm{two}}-ab+b^2)\hfill \end{array}$ , where a and b correspond algebraic expressions. and difference of cubes $\begin{array}{l}{a}^3-b^3\hfill \\ =(a-b)(a^2+ab+b^2)\hfill \end{array}$ , where a and b represent algebraic expressions. :

$$\begin{array}{lll}\hfill a^{\mathrm{three}}+b^{\mathrm{iii}}& =& \left(a+b\right)\left(a^{\mathrm{two}}-ab+b^2\right)\hfill \\ \hfill a^3-b^3& =& \left(a-b\right)\left(a^2+ab+b^{\mathrm{ii}}\right)\hfill \end{array}$$

Nosotros tin can verify these formulas by multiplying.

$$\begin{array}{ccc}\hfill \left(a+b\right)\left(a^2-ab+b^{\mathrm{two}}\right)& =& a^3-a^{2}b+a{b}^2+a^{2}b-a{b}^{\mathrm{ii}}+b^{\mathrm{iii}}\hfill \\ \hfill & =& a^3+b^{\mathrm{iii}}✓\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \left(a-b\right)\left(a^2+ab+b^{\mathrm{two}}\right)& =& a^3+a^{2}b+a{b}^{\mathrm{ii}}-a^{2}b-a{b}^{\mathrm{ii}}-b^3\hfill \\ \hfill & =& a^3-b^{\mathrm{three}}✓\hfill \end{array}$$

The process for factoring sums and differences of cubes is very similar to that of differences of squares. We commencement identify a and b and then substitute into the appropriate formula. The separate formulas for the sum and departure of cubes allow usa to e'er cull a and b to be positive.

Example x

Factor: $x^{\mathrm{three}}-\mathrm{viii}{y}^3.$

Solution:

First, identify this binomial equally a difference of cubes.

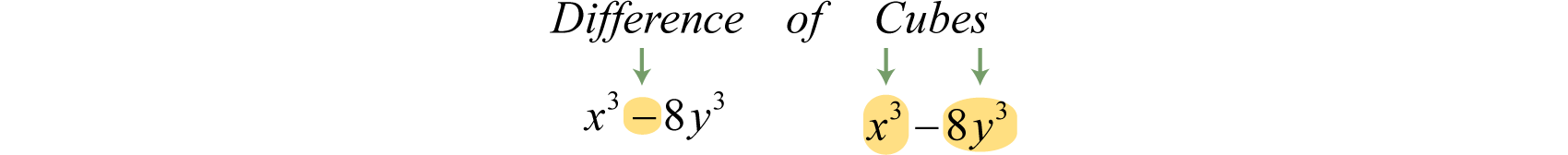
Side by side, identify what is being cubed.

$$x^3-8y^3={\left(\mathrm{ten}\right)}^3-{\left(2y\right)}^{\mathrm{iii}}$$

In this case, $a=x$ and $b=2y.$ Substitute into the difference of cubes formula.

$$\begin{array}{cccccccccccccc}\hfill a^3+b^3& =& (\hfill & a& -& b& )& (& a^2& +& a\cdot b& +& b^2& )\\ \hfill & & & \downarrow & & \downarrow & & & \downarrow & & \downarrow \downarrow & & \downarrow & \\ \hfill {\mathrm{10}}^3-8y^{\mathrm{three}}& =& (\hfill & x& -& \mathrm{two}y& )& (& {\left(\mathrm{ten}\right)}^2& +& x\cdot \mathrm{ii}y& +& {\left(\mathrm{ii}y\right)}^2& )\\ \hfill & =& (\hfill & x& -& 2y& )& (& x^2& +& 2xy& +& 4y^2& )\end{array}$$

Nosotros can check this factorization by multiplying.

$$\begin{array}{ccc}\hfill \left(x-2y\right)\left({\mathrm{10}}^2+2xy+4y^2\right)& =& x^3+\mathrm{ii}{x}^{2}y+4\mathrm{10}{y}^{\mathrm{two}}-2{\mathrm{10}}^{\mathrm{two}}y-4\mathrm{10}{y}^{\mathrm{two}}-8y^{\mathrm{three}}\hfill \\ \hfill & =& x^3+\mathrm{ii}{x}^{2}y+4x{y}^2-2x^{2}y-4x{y}^2-\mathrm{viii}{y}^3\hfill \\ \hfill & =& x^{\mathrm{iii}}-8y^3✓\hfill \end{array}$$

Reply: $\left(x-2y\right)\left(x^{\mathrm{ii}}+2xy+4y^2\right)$

It may be the case that the terms of the binomial have a common factor. If so, it will exist difficult to identify it as a special binomial until we first factor out the GCF.

Example xi

Cistron: $81x^{4}y+3x{y}^4.$

Solution:

The terms are non perfect squares or perfect cubes. However, notice that they practise have a mutual factor. First, factor out the GCF, $3xy.$

$$81x^{4}y+3x{y}^4=3\mathrm{ten}y\left(27{\mathrm{10}}^{\mathrm{iii}}+y^3\right)$$

The resulting binomial factor is a sum of cubes with $a=\mathrm{iii}x$ and $b=y.$

$$\begin{array}{ccc}\hfill 81x^{\mathrm{four}}y+3\mathrm{ten}{y}^{\mathrm{four}}& =& \mathrm{iii}xy\left(27x^3+y^3\right)\hfill \\ \hfill & =& 3\mathrm{ten}y\left(3\mathrm{10}+y\right)\left(9x^2-3xy+y^{\mathrm{ii}}\right)\hfill \end{array}$$

Answer: $3\mathrm{10}y\left(3x+y\right)\left(9x^2-\mathrm{iii}xy+y^2\right)$

When the degree of the special binomial is greater than two, we may need to apply the formulas multiple times to obtain a complete factorization. A polynomial is completely factoredA polynomial that is prime or written as a product of prime number polynomials. when information technology is prime or is written as a product of prime number polynomials.

Example 12

Factor completely: ${\mathrm{10}}^{\mathrm{iv}}-81y^{\mathrm{iv}}.$

Solution:

Outset, identify what is being squared.

$$x^4-81y^4={\left(\right)}^2-{\left(\right)}^{\mathrm{two}}$$

To do this, remember the power rule for exponents, ${\left(x^{\mathrm{1000}}\right)}^n=x^{m\mathrm{due\; north}}.$ When exponents are raised to a ability, multiply them. With this in mind, we find

$$x^{\mathrm{iv}}-81y^4={\left(x^2\right)}^{\mathrm{two}}-{\left(9y^2\right)}^{\mathrm{two}}$$

Therefore, $a=x^{\mathrm{two}}$ and $b=9y^2.$ Substitute into the formula for divergence of squares.

$$x^4-81y^{\mathrm{iv}}=\left(x^{\mathrm{ii}}+9y^2\right)\left({\mathrm{10}}^2-9y^{\mathrm{ii}}\right)$$

At this signal, notice that the gene $\left(x^2-9y^{\mathrm{two}}\right)$ is itself a departure of two squares and thus tin can be further factored using $a={\mathrm{10}}^2$ and $b=3y.$ The factor $\left(x^2+9y^2\right)$ is prime and cannot be factored using existent numbers.

$$\begin{array}{ccc}\hfill {\mathrm{ten}}^4-81y^4& =& \left(x^2+9y^2\right)\left({\mathrm{ten}}^2-9y^2\right)\hfill \\ \hfill & =& \left({\mathrm{ten}}^{\mathrm{two}}+9y^2\right)\left(x+3y\right)\left(x-3y\right)\hfill \end{array}$$

Reply: $\left(x^2+9y^2\right)\left(x+3y\right)\left(\mathrm{ten}-3y\right)$

When factoring, e'er look for resulting factors to factor further.

Example 13

Factor completely: $64x^6-y^{\mathrm{half\; dozen}}.$

Solution:

This binomial is both a difference of squares and divergence of cubes.

$$\begin{array}{lll}\hfill 64x^{\mathrm{vi}}-y^6& =\hfill & {\left(4x^2\right)}^3-{\left(y^2\right)}^{3}Diff\mathrm{east}r\mathrm{eastward}\mathrm{due\; north}ceofcube\mathrm{southward}\hfill \\ \hfill 64{\mathrm{ten}}^{\mathrm{half-dozen}}-y^{\mathrm{vi}}& =\hfill & {\left(8x^3\right)}^2-{\left(y^3\right)}^{2}Diff\mathrm{due\; east}r\mathrm{east}\mathrm{due\; north}c\mathrm{east}ofsquares\hfill \end{array}$$

When confronted with a binomial that is a deviation of both squares and cubes, as this is, make it a rule to cistron using difference of squares first. Therefore, $a=8x^3$ and $b=y^3.$ Substitute into the divergence of squares formula.

$$64x^{\mathrm{half-dozen}}-y^6=\left(8{\mathrm{10}}^3+y^3\right)\left(8x^{\mathrm{three}}-y^3\right)$$

The resulting two binomial factors are sum and difference of cubes. Each can be factored farther. Therefore, we accept

The trinomial factors are prime and the expression is completely factored.

Answer: $\left(2\mathrm{ten}+y\right)\left(\mathrm{iv}{x}^2-\mathrm{ii}xy+y^{\mathrm{ii}}\right)\left(\mathrm{two}x-y\right)\left(4x^2+2xy+y^2\right)$

As an exercise, factor the previous instance as a difference of cubes kickoff so compare the results. Why practice you think we go far a rule to factor using difference of squares outset?

Attempt this! Gene: $a^6{b}^{\mathrm{six}}-1$

Answer: $\left(ab+1\right)\left(a^2{b}^2-ab+\mathrm{i}\right)\left(ab-1\right)\left(a^2{b}^2+ab+\mathrm{ane}\right)$

Key Takeaways

• The GCF of two or more monomials is the product of the GCF of the coefficients and the mutual variable factors with the smallest power.
• If the terms of a polynomial accept a greatest common gene, so factor out that GCF using the distributive holding. Divide each term of the polynomial by the GCF to make up one's mind the terms of the remaining factor.
• Some four-term polynomials can be factored by grouping the first two terms and the last two terms. Gene out the GCF of each group and then cistron out the common binomial factor.
• When factoring by grouping, you sometimes take to rearrange the terms to detect a common binomial factor. Later factoring out the GCF, the remaining binomial factors must exist the same for the technique to work.
• When factoring special binomials, the first step is to identify it as a sum or departure. Once we identify the binomial, nosotros and so decide the values of a and b and and then substitute into the appropriate formula.
• If a binomial is both a difference of squares and cubes, and so first factor it as a deviation of squares.

Topic Exercises

Office A: Factoring out the GCF

Determine the GCF of the given expressions.

1. $9x^{\mathrm{v}}$ , $27x^{\mathrm{two}}$ , $15x^{\mathrm{seven}}$

2. $20y^4$ , $12y^7$ , $16y^3$

3. $\mathrm{fifty}{x}^2{y}^3$ , $35\mathrm{ten}{y}^{\mathrm{iii}}$ , $10x^3{y}^{\mathrm{two}}$

4. $12x^{\mathrm{seven}}{y}^2$ , $36{\mathrm{10}}^4{y}^{\mathrm{two}}$ , $18x^{3}y$

5. $15a^7{b}^2{c}^5$ , $75a^7{b}^{\mathrm{three}}c$ , $45a{b}^4{c}^3$

6. $12a^6{b}^{\mathrm{three}}{c}^2$ , $48ab{c}^3$ , $125a^2{b}^{3}c$

7. $60{\mathrm{ten}}^2{\left(2x-\mathrm{one}\right)}^{\mathrm{three}}$ , $42\mathrm{ten}{\left(2x-\mathrm{ane}\right)}^{\mathrm{three}}$ , $6{\mathrm{ten}}^3\left(2x-\mathrm{ane}\right)$

8. $14y^{\mathrm{v}}{\left(y-8\right)}^{\mathrm{two}}$ , $28y^{\mathrm{ii}}\left(y-8\right)$ , $35y{\left(y-8\right)}^3$

9. $10a^2{b}^{\mathrm{iii}}{\left(a+b\right)}^5$ , $48a^5{b}^{\mathrm{ii}}{\left(a+b\right)}^2$ , $26a{b}^5{\left(a+b\right)}^{\mathrm{three}}$

10. $45a{b}^{\mathrm{seven}}{\left(a-b\right)}^7$ , $36a^{\mathrm{two}}{b}^2{\left(a-b\right)}^3$ , $63a^{\mathrm{four}}{b}^3{\left(a-b\right)}^2$

Determine the missing factor.

11. $18x^4-6x^3+2x^2=\mathrm{ii}{\mathrm{10}}^{\mathrm{ii}}\left(?\right)$

12. $6{\mathrm{ten}}^5-9{\mathrm{10}}^3-3\mathrm{10}=3\mathrm{10}\left(\text{}\text{}\text{}\text{}\text{}?\right)$

13. $-10y^6+6y^{\mathrm{four}}-\mathrm{iv}{y}^{\mathrm{two}}=-2y^2\left(?\right)$

14. $-27y^9-9y^6+3y^3=-3y^3\left(?\right)$

15. $12x^3{y}^{\mathrm{ii}}-8x^2{y}^3+\mathrm{viii}xy=4xy\left(?\right)$

16. $10x^4{y}^3-50x^{\mathrm{three}}{y}^2+\mathrm{fifteen}{\mathrm{10}}^{\mathrm{ii}}{y}^2=5\mathrm{ten}y\left(?\right)$

17. $14a^{\mathrm{iv}}{b}^{\mathrm{v}}-21a^3{b}^4-7a^2{b}^3=7a^{\mathrm{two}}{b}^3\left(?\right)$

18. $\mathrm{fifteen}{a}^5{b}^4+\mathrm{nine}{a}^4{b}^2-\mathrm{three}{a}^{\mathrm{two}}b=3a^{2}b\left(?\right)$

19. $x^{3\mathrm{northward}}+{\mathrm{ten}}^{2n}+{\mathrm{ten}}^n={\mathrm{10}}^{\mathrm{northward}}\left(?\right)$

20. $y^{4n}+y^{3\mathrm{northward}}-y^{\mathrm{ii}n}=y^{\mathrm{two}n}\left(?\right)$

Factor out the GCF.

21. $12x^4-\mathrm{xvi}{x}^{\mathrm{iii}}+4x^2$

22. $15{\mathrm{ten}}^5-10x^4-5x^{\mathrm{three}}$

23. $20y^8+28y^6+\mathrm{forty}{y}^3$

24. $18y^7-24y^5-30y^3$

25. $\mathrm{ii}{a}^{\mathrm{four}}{b}^3-6a^3{b}^{\mathrm{two}}+\mathrm{viii}{a}^{\mathrm{ii}}b$

26. $28a^{\mathrm{three}}{b}^3-21a^{\mathrm{ii}}{b}^4-\mathrm{fourteen}a{b}^5$

27. $\mathrm{ii}{x}^3{y}^{\mathrm{five}}-\mathrm{four}{x}^4{y}^{\mathrm{iv}}+x^{\mathrm{two}}{y}^{\mathrm{three}}$

28. $3{\mathrm{10}}^{5}y-\mathrm{two}{x}^4{y}^{\mathrm{two}}+x^{\mathrm{iii}}{y}^{\mathrm{iii}}$

29. $\mathrm{five}{x}^2\left(\mathrm{ii}x+3\right)-3\left(2x+3\right)$

30. $y^2\left(y-\mathrm{i}\right)+9\left(y-1\right)$

31. $9x^2\left(3\mathrm{10}-\mathrm{ane}\right)+\left(3x-1\right)$

32. $\mathrm{seven}{y}^2\left(5y+2\right)-\left(5y+2\right)$

33. ${\mathrm{ten}}^{5\mathrm{northward}}-x^{3n}+{\mathrm{ten}}^n$

34. $y^{\mathrm{vi}n}-y^{3\mathrm{north}}-y^{2\mathrm{north}}$

Part B: Factoring by Grouping

Factor by grouping.

35. $\mathrm{ii}{x}^3+\mathrm{three}{x}^2+2\mathrm{ten}+3$

36. $5x^3+25{\mathrm{ten}}^2+\mathrm{ten}+\mathrm{five}$

37. $6x^{\mathrm{three}}-3x^2+4x-\mathrm{two}$

38. $3{\mathrm{10}}^3-2x^2-\mathrm{xv}\mathrm{ten}+\mathrm{x}$

39. ${\mathrm{10}}^{\mathrm{iii}}-x^{\mathrm{two}}-3x+3$

40. $\mathrm{half\; dozen}{x}^3-\mathrm{xv}{x}^{\mathrm{ii}}-\mathrm{two}\mathrm{10}+5$

41. $2x^{\mathrm{iii}}+7x^2-\mathrm{x}x-35$

42. $3x^3-{\mathrm{ten}}^2+24x-8$

43. $14y^{\mathrm{four}}+10y^{\mathrm{three}}-\mathrm{vii}y-\mathrm{v}$

44. $5y^4+2y^3+\mathrm{twenty}y+\mathrm{viii}$

45. ${\mathrm{ten}}^{4n}+{\mathrm{10}}^{3\mathrm{northward}}+2x^n+2$

46. $x^{5n}+x^{\mathrm{three}\mathrm{northward}}+3x^{\mathrm{ii}n}+3$

47. $x^{\mathrm{iii}}-x^{2}y+x{y}^2-y^3$

48. ${\mathrm{ten}}^3+x^{\mathrm{ii}}y-2\mathrm{10}{y}^2-2y^3$

49. $3x^{\mathrm{three}}{y}^{\mathrm{ii}}+9x^2{y}^{\mathrm{iii}}-x-3y$

50. $2x^3{y}^3-x^2{y}^3+2\mathrm{ten}-y$

51. $a^{2}b-\mathrm{four}a{b}^{\mathrm{two}}-3a+12b$

52. $a^{2}b+3a{b}^2+5a+\mathrm{xv}b$

53. $a^4+a^{\mathrm{ii}}{b}^3+a^{2}b+b^4$

54. $a^{\mathrm{iii}}b+2a^2+\mathrm{iii}a{b}^4+\mathrm{half-dozen}{b}^{\mathrm{three}}$

55. $\mathrm{iii}ax+\mathrm{x}by-5ay-\mathrm{half-dozen}bx$

56. $a^{2}x-\mathrm{v}{b}^{\mathrm{ii}}y-5a^{\mathrm{ii}}y+b^{2}x$

57. ${\mathrm{ten}}^{\mathrm{iv}}{y}^2-{\mathrm{10}}^3{y}^3+x^2{y}^4-x{y}^5$

58. $2x^5{y}^2+\mathrm{four}{x}^{\mathrm{iv}}{y}^2+18x^{3}y+36{\mathrm{ten}}^{\mathrm{ii}}y$

59. $a^5{b}^2+a^4{b}^{\mathrm{four}}+a^3{b}^3+a^{\mathrm{ii}}{b}^5$

60. $3a^{\mathrm{six}}b+3a^{\mathrm{five}}{b}^2+9a^4{b}^2+9a^3{b}^{\mathrm{iii}}$

Part C: Factoring Special Binomials

Cistron.

61. $x^2-64$

62. $x^2-100$

63. $\mathrm{ix}-4y^2$

64. $25-y^{\mathrm{two}}$

65. ${\mathrm{10}}^2-81y^2$

66. ${\mathrm{ten}}^{\mathrm{ii}}-49y^2$

67. $a^{\mathrm{ii}}{b}^2-\mathrm{iv}$

68. $1-9a^{\mathrm{ii}}{b}^{\mathrm{two}}$

69. $a^{\mathrm{two}}{b}^2-c^{\mathrm{two}}$

70. $\mathrm{iv}{a}^2-b^{\mathrm{ii}}{c}^2$

71. $x^{\mathrm{four}}-64$

72. $36-y^4$

73. ${\left(\mathrm{ii}\mathrm{10}+5\right)}^2-x^2$

74. ${\left(3\mathrm{10}-\mathrm{v}\right)}^{\mathrm{ii}}-x^2$

75. $y^2-{\left(y-3\right)}^{\mathrm{ii}}$

76. $y^2-{\left(\mathrm{two}y+\mathrm{i}\right)}^2$

77. ${\left(2x+5\right)}^2-{\left(x-3\right)}^2$

78. ${\left(3x-1\right)}^{\mathrm{ii}}-{\left(2x-\mathrm{iii}\right)}^2$

79. $x^4-16$

80. $81{\mathrm{10}}^4-1$

81. $x^4{y}^4-1$

82. $x^{\mathrm{four}}-y^{\mathrm{iv}}$

83. $x^8-y^8$

84. $y^8-\mathrm{ane}$

85. $x^{2n}-y^{2n}$

86. ${\mathrm{ten}}^{2n}{y}^{2n}-4$

87. ${\mathrm{ten}}^{4n}-y^{\mathrm{four}\mathrm{north}}$

88. ${\mathrm{ten}}^{4\mathrm{northward}}{y}^{\mathrm{iv}n}-\mathrm{sixteen}$

89. $x^3-27$

90. $8x^{\mathrm{iii}}-125$

91. $\mathrm{eight}{y}^3+27$

92. $64x^{\mathrm{iii}}+343$

93. $x^{\mathrm{iii}}-y^{\mathrm{three}}$

94. $x^{\mathrm{iii}}+y^3$

95. $8a^3{b}^{\mathrm{three}}+1$

96. $27a^3-\mathrm{eight}{b}^3$

97. $x^{\mathrm{three}}{y}^3-125$

98. $216x^3+y^3$

99. $x^3+{\left(x+3\right)}^{\mathrm{iii}}$

100. $y^{\mathrm{three}}-{\left(\mathrm{ii}y-1\right)}^3$

101. ${\left(2x+1\right)}^3-x^3$

102. ${\left(3y-5\right)}^3-y^3$

103. ${\mathrm{10}}^{\mathrm{iii}n}-y^{\mathrm{iii}\mathrm{northward}}$

104. $x^{\mathrm{iii}\mathrm{north}}+y^{3n}$

105. $a^6+64$

106. $64a^6-1$

107. ${\mathrm{ten}}^6-y^6$

108. $x^6+y^{\mathrm{vi}}$

109. ${\mathrm{10}}^{\mathrm{half-dozen}\mathrm{due\; north}}-y^{6n}$

110. $x^{6\mathrm{north}}+y^{6n}$

111. Given $f\left(\mathrm{ten}\right)=2x-\mathrm{i}$ , evidence that $\left(f+f\right)\left(\mathrm{10}\right)=2f\left(\mathrm{10}\right).$

112. Given $f\left(x\right)={\mathrm{10}}^{\mathrm{two}}-3x+\mathrm{two}$ , evidence that $\left(f+f\right)\left(x\right)=2f\left(x\right).$

113. Given $f\left(\mathrm{10}\right)=\mathrm{thousand}x+b$ , show that $\left(f+f\right)\left(x\right)=2f\left(\mathrm{10}\right).$

114. Given $f\left(x\right)=a{x}^2+b\mathrm{ten}+c$ , show that $\left(f+f\right)\left(x\right)=2f\left(\mathrm{ten}\right).$

115. Given $f\left(\mathrm{ten}\right)=a{x}^2+bx+c$ , show that $\left(f-f\right)\left(x\right)=0.$

116. Given $f\left(\mathrm{10}\right)=mx+b$ , show that $\left(f-f\right)\left(x\right)=0.$

Part D: Word Board

117. What tin be said nigh the degree of a gene of a polynomial? Give an case.

118. If a binomial falls into both categories, difference of squares and departure of cubes, which would exist best to use for factoring, and why? Create an example that illustrates this situation and factor it using both formulas.

119. Write your ain examples for each of the 3 special types of binomial. Factor them and share your results.

Answers

1. $3x^2$

3. $5x{y}^2$

5. $15a{b}^{\mathrm{ii}}c$

7. $\mathrm{six}\mathrm{10}\left(2x-1\right)$

9. $2a{b}^2{\left(a+b\right)}^2$

11. $\left(9x^2-\mathrm{three}x+1\right)$

13. $\left(5y^{\mathrm{four}}-3y^2+2\right)$

15. $\left(3{\mathrm{ten}}^{2}y-2x{y}^{\mathrm{ii}}+2\right)$

17. $\left(\mathrm{ii}{a}^2{b}^2-3ab-1\right)$

19. $\left({\mathrm{10}}^{2n}+x^{\mathrm{northward}}+1\right)$

21. $4x^2\left(3x^2-4\mathrm{10}+1\right)$

23. $4y^3\left(5y^5+7y^{\mathrm{iii}}+10\right)$

25. $2a^{2}b\left(a^2{b}^2-\mathrm{iii}ab+\mathrm{iv}\right)$

27. ${\mathrm{ten}}^{\mathrm{two}}{y}^3\left(2x{y}^{\mathrm{two}}-4x^{\mathrm{two}}y+1\right)$

29. $\left(\mathrm{ii}x+3\right)\left(\mathrm{v}{\mathrm{10}}^2-3\right)$

31. $\left(3x-\mathrm{ane}\right)\left(\mathrm{nine}{x}^2+1\right)$

33. $x^n\left(x^{4n}-x^{\mathrm{two}\mathrm{northward}}+1\right)$

35. $\left(\mathrm{two}x+3\right)\left({\mathrm{ten}}^{\mathrm{two}}+1\right)$

37. $\left(\mathrm{ii}x-1\right)\left(\mathrm{iii}{x}^{\mathrm{ii}}+2\right)$

39. $\left(x-1\right)\left(x^2-3\right)$

41. $\left(2x+7\right)\left(x^2-5\right)$

43. $\left(7y+5\right)\left(\mathrm{ii}{y}^{\mathrm{iii}}-1\right)$

45. $\left(x^n+\mathrm{ane}\right)\left(x^{3\mathrm{north}}+2\right)$

47. $\left(x-y\right)\left(x^{\mathrm{two}}+y^{\mathrm{two}}\right)$

49. $\left(x+3y\right)\left(3x^2{y}^{\mathrm{ii}}-1\right)$

51. $\left(a-4b\right)\left(ab-\mathrm{iii}\right)$

53. $\left(a^2+b\right)\left(a^{\mathrm{ii}}+b^{\mathrm{iii}}\right)$

55. $\left(a-2b\right)\left(3x-5y\right)$

57. $x{y}^2\left(x-y\right)\left(x^{\mathrm{ii}}+y^2\right)$

59. $a^{\mathrm{ii}}{b}^2\left(a^2+b\right)\left(a+b^{\mathrm{ii}}\right)$

61. $\left(\mathrm{10}+\mathrm{eight}\right)\left(\mathrm{ten}-\mathrm{viii}\right)$

63. $\left(3+2y\right)\left(\mathrm{iii}-\mathrm{two}y\right)$

65. $\left(\mathrm{ten}+9y\right)\left(\mathrm{10}-9y\right)$

67. $\left(ab+2\right)\left(ab-2\right)$

69. $\left(ab+c\right)\left(ab-c\right)$

71. $\left(x^2+8\right)\left({\mathrm{10}}^2-8\right)$

73. $\left(\mathrm{three}\mathrm{ten}+5\right)\left(\mathrm{10}+5\right)$

75. $3\left(\mathrm{two}y-3\right)$

77. $\left(\mathrm{iii}\mathrm{10}+2\right)\left(x+8\right)$

79. $\left(x^{\mathrm{two}}+4\right)\left(x+2\right)\left(x-2\right)$

81. $\left(x^2{y}^2+1\right)\left(xy+1\right)\left(xy-\mathrm{ane}\right)$

83. $\left(x^4+y^4\right)\left(x^2+y^2\right)\left(\mathrm{10}+y\right)\left(x-y\right)$

85. $\left(x^n+y^n\right)\left(x^n-y^{\mathrm{northward}}\right)$

87. $\left({\mathrm{10}}^{2\mathrm{north}}+y^{2n}\right)\left(x^n+y^{\mathrm{due\; north}}\right)\left(x^n-y^n\right)$

89. $\left(x-\mathrm{three}\right)\left(x^2+3x+9\right)$

91. $\left(\mathrm{ii}y+3\right)\left(4y^{\mathrm{two}}-6y+9\right)$

93. $\left(x-y\right)\left(x^{\mathrm{ii}}+xy+y^{\mathrm{ii}}\right)$

95. $\left(\mathrm{two}ab+\mathrm{i}\right)\left(\mathrm{iv}{a}^2{b}^{\mathrm{ii}}-2ab+1\right)$

97. $\left(xy-\mathrm{v}\right)\left(x^2{y}^{\mathrm{ii}}+5\mathrm{10}y+25\right)$

99. $\left(2\mathrm{ten}+3\right)\left(x^2+3\mathrm{10}+\mathrm{ix}\right)$

101. $\left(x+1\right)\left(\mathrm{seven}{\mathrm{10}}^2+5\mathrm{ten}+1\right)$

103. $\left(x^n-y^{\mathrm{north}}\right)\left(x^{2n}+{\mathrm{ten}}^n{y}^n+y^{\mathrm{two}n}\right)$

105. $\left(a^{\mathrm{two}}+\mathrm{iv}\right)\left(a^{\mathrm{iv}}-4a^2+\mathrm{sixteen}\right)$

107. $\left(x+y\right)\left({\mathrm{10}}^{\mathrm{two}}-xy+y^2\right)\left(\mathrm{10}-y\right)\left(x^2+\mathrm{ten}y+y^2\right)$

109. $$\begin{array}{l}\left(x^{\mathrm{due\; north}}+y^n\right)\left(x^{\mathrm{ii}n}-x^{\mathrm{north}}{y}^{\mathrm{north}}+y^{2n}\right)\hfill \\ \times \left(x^n-y^{\mathrm{due\; north}}\right)\left(x^{2n}+x^n{y}^n+y^{2\mathrm{north}}\right)\hfill \end{array}$$

111. Respond may vary

113. Reply may vary

115. Answer may vary

117. Answer may vary

119. Answer may vary

Source: https://saylordotorg.github.io/text_intermediate-algebra/s07-02-factoring-polynomials.html

Posted by: hillneho1973.blogspot.com

Share this post